0. Research Objective

To explore the impact of freeway evolution on socioeconomic attributes. Specifically, it jointly consider free density and freeway nertwork topology to study their impact on: a.socio-economic indicators b. county-level POI dentsities c. POI dentieis along the freeway

1. Data and variables

1.1 Research Area and data

The reseach Area is the Fujian Province, the granularity of the analysis unit is county-level, there are 61 analysis unit in total.

The data includes:

Freeway netowrk data, obtained from OpenstreetMap
POI data, obtained from Amap API.
Social-economic data, obtained from China Statistical Yearbook(county-level)

1.2 Variables

Independent variables: Freeway density, freeway network topology attributes, including degree centrality, closeness centrality, betweeness centrality.
Dependent variables: Three categories, including Socio-economic attributes, county-level POI densities, POI densities along the freeway.

2. Methodology

Multiscale geographically and temporally weighted regression (MGTWR) is employed:

\[Y(i) = \beta_{bw\, s_{0},\, bw\, t_{0}}(i) + \sum_{m=1}^{n} \beta_{bw\, s_{m},\, bw\, t_{m}}(i)\, X_{m}(i) + \varepsilon(i)\]

where $i$ represents the $i$th sample characterized by specific spatiotemporal coordinates ( $u_i$,$v_i$,$t_i$ ), $Y(i)$ signifies the dependent variable of interest, $X_m(i)$ denotes the th independent variable.

3. Results and conclusion

This below figure illustrates the estimated coefficients associated with the four independent variables concerning the primary industry output. Each coefficient depicted in the figure signifies the mean value across a span of four years (i.e., 2018–2021) within a distinct fundamental analysis unit.

The color indicates the relative magnitude of the coefficient, ranging from red (high positive values) to blue (high negative values). The upward triangle symbol implies that the estimated coefficient for a given unit exhibits a consistent and monotonic increase over the four-year period. Conversely, the downward triangle symbol is employed to denote estimated coefficients that exhibit a steady decrease across the same temporal span. Meanwhile, the dot symbol is utilized to represent cases where the estimated coefficient does not exhibit a discernible monotonic trend.

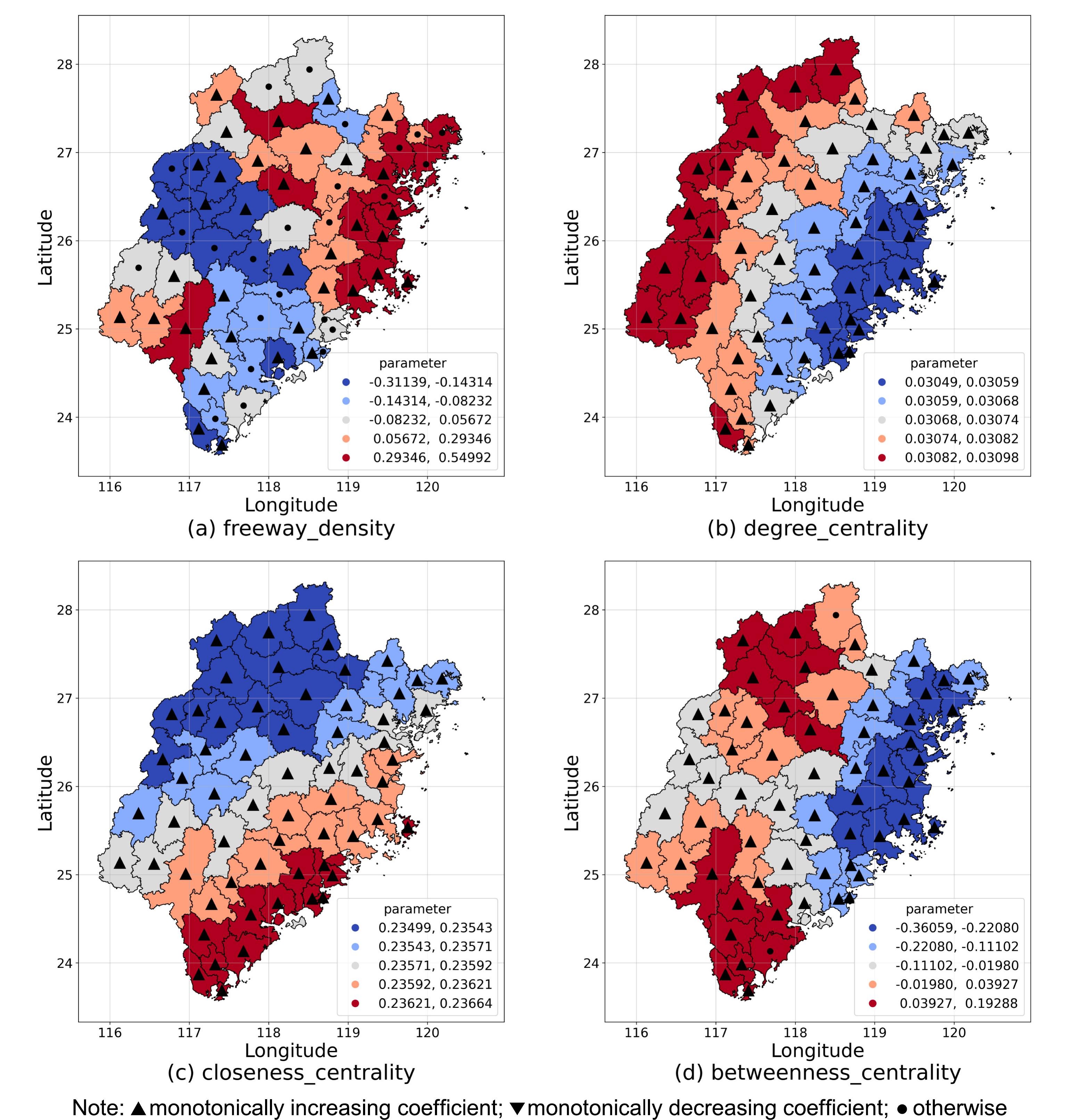
Impact on the primary industry output. — Impact on the primary industry output

As depicted in the above picture, the influence of freeway density in driving the expansion of the primary industry becomes particularly significant along the northeast coast. In these regions, the primary industry is largely focused on the advancement of aquaculture and leisure agriculture (i.e., the fusion of recreational and tourism activities within agricultural contexts). The accessibility of freeways within these regions may play a pivotal role in expediting the transportation of aquatic products and facilitating the movement of individuals engaging in leisure agricultural activities. This situation augments the economic impetus generated by the freeway infrastructure along the northeast coast. Additionally, the positive coefficient linked to freeway density exhibits a trend of growth across Fujian Province. This pattern suggests that the economic stimulus from freeways might possess a scale effect, wherein the impact amplifies with an increase in the density of freeway.

During the new route planning process, an evaluation strategy that considers the characteristics of the freeway network can assist decision-makers in analyzing how to enhance network efficiency through new route construction, instead of focusing solely on the impact of increased mileage.

Degree centrality, which facilitates direct regional communication, has the potential to enhance socio-economic indicators and foster the aggregation of POIs both within regions and along freeway routes. Conversely, network metrics that improve regional accessibility, such as closeness centrality, and those that promote regions as bridges for inter-regional communication, such as betweenness centrality, tend to result in a decline in socio-economic development dynamics. This phenomenon can be explained by the fact that regions serving as hubs within the freeway network typically have significant economic growth potential, whereas regions in intermediary positions within the freeway network serve as conduits for resource flow, placing them at a disadvantage in terms of local economic growth prospects.